Different sources of uncertainty arise in the study of structural engineering analysis, where the inputs and parameters can be uncertain due to different reasons, e.g., irregularities in the material manufacturing, variations of material properties or lack of knowledge on the loading conditions. Traditionally, uncertainties are treated in a post-processing manner by safety factors, etc., which have been developed from engineering empirical experience. However, there is a limited physical understanding behind, which often guides to un-economical design of structures. To overcome these limitations, novel computational techniques for the treatment of stochastic differential equations have been developed, where the random parameters are treated as random variables or, more generally, modeled as random fields. This approach is referred to as the Stochastic Finite Element Method (SFEM). The main significance of the SFEM is the representation of the uncertainties related to the physical model.

During our stochastic finite element methods module, you will be trained to go beyond deterministic mechanical predictions. Intrusive and non-intrusive methods will be discussed in detail, providing you with a new set of tools indispensable for planning and analysis in many engineering applications.

 The following issues will be discussed:

• Motivation for stochastic computational techniques e.g. for non-linear system response
• Statistical basics and stochastic methods for the treatment of random variables, random fields and random processes
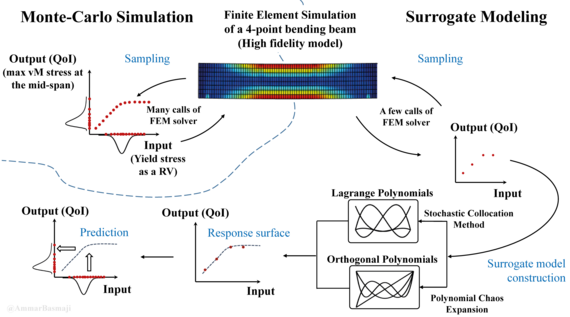
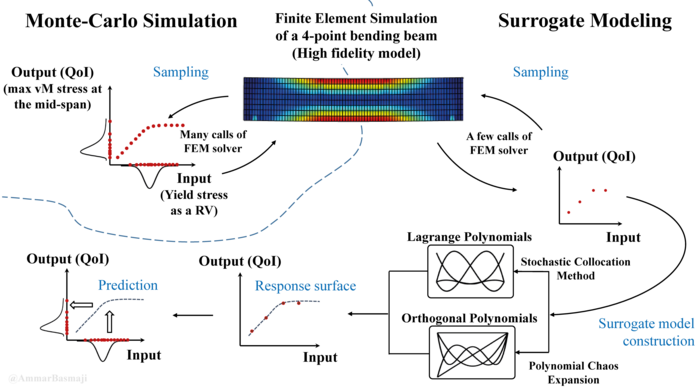
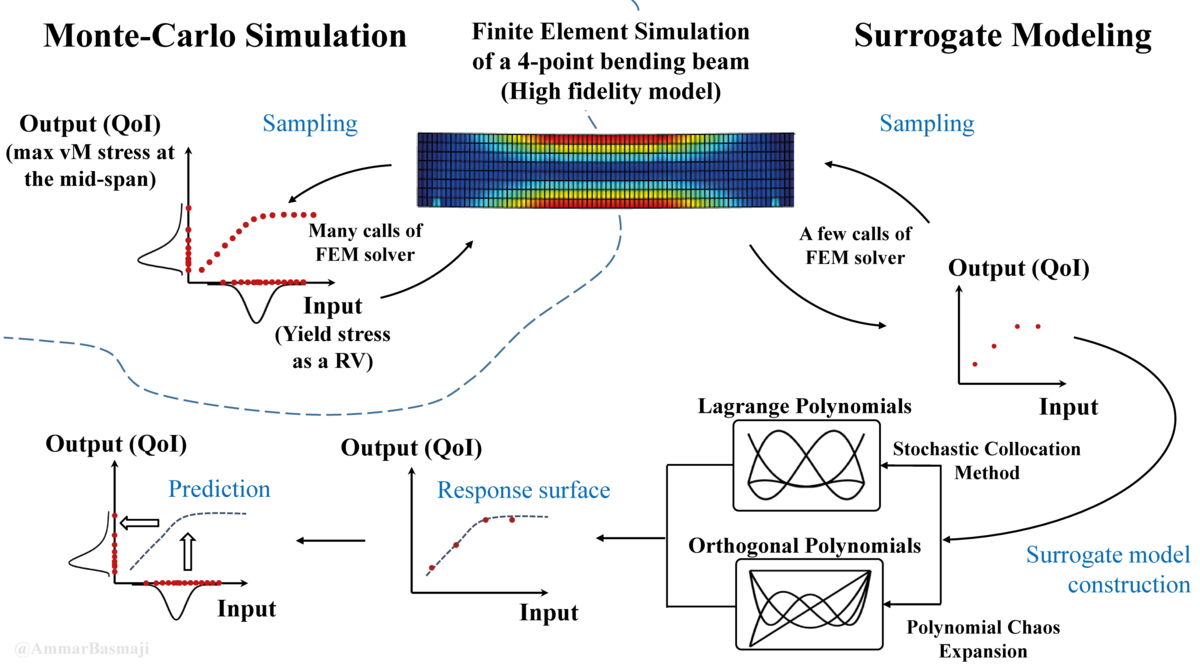
• Computational sampling techniques, e.g. Monte-Carlo methods, stochastic collocation techniques, computational aspects (e.g. parallelization, intrusive vs. non-intrusive etc
• Inverse problems, identification of parameters, experimental uncertainty analysis
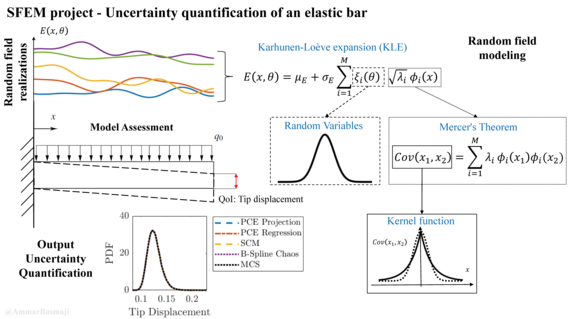
• Discretization techniques for random fields and random processes
• Spectral Stochastic Finite Element Method – Theory, Implementation and Investigation
• Alternative concepts on modelling stochastic processes, e.g. Fokker-Planck-representation, computational aspects
• Model order reduction for mechanical problems with uncertainties
• Postprocessing, Quantity of Interest: Preparation and interpretation of computed results

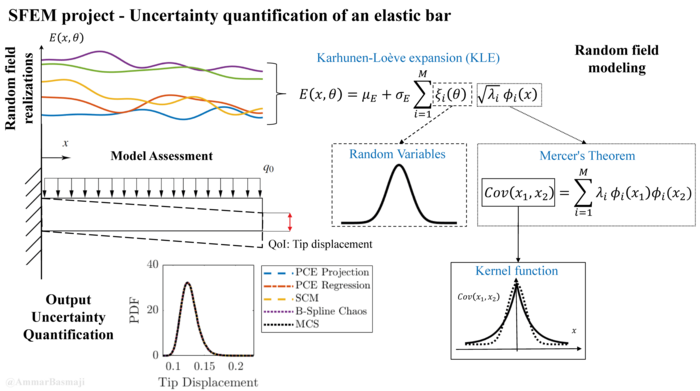
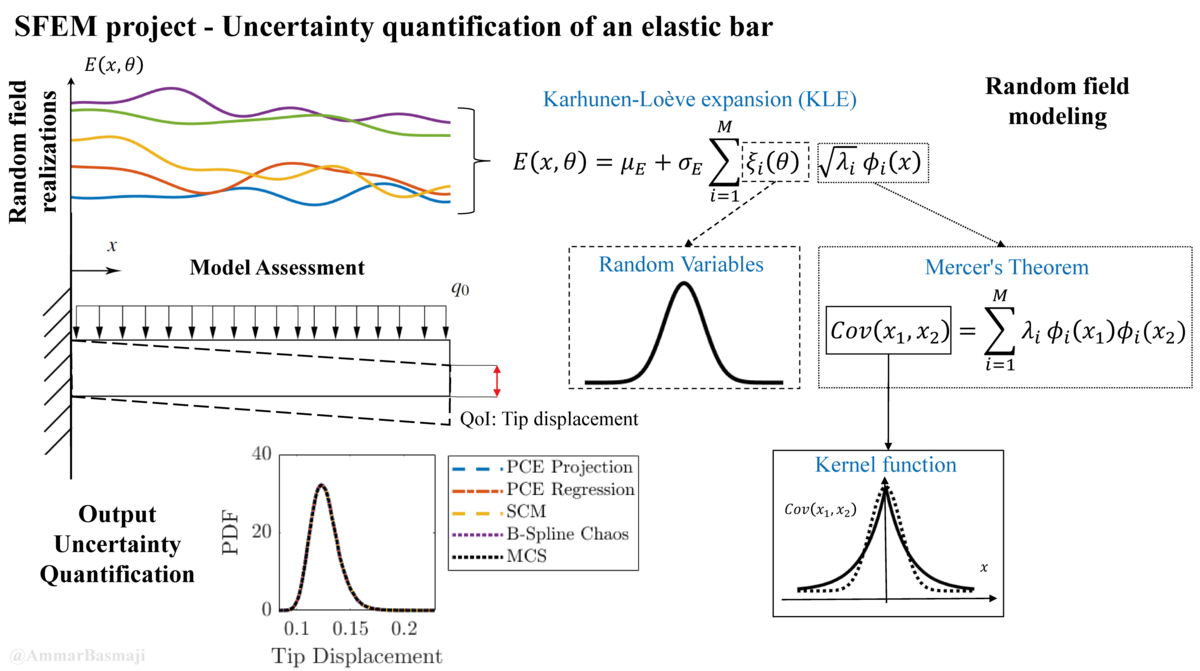
This course is strongly related to our current research activities at IBNM and enriched by contributions of the doctoral researchers, who will address their current research activities and open questions. Thus, the goal is to guide the students to active scientific research strategies and methods.

This class is designed for a project-based learning experience, i.e., you must solve a small research task considering scientific standards. Thus, the evaluation is based on one homework and a final project, both presented as reports written under the standards of a research paper, followed by an oral presentation held as a seminar for all the other participants of the course.

The project topic is established in accordance with the own student interests.

References

• R.G. Ghanem and P.D. Spanos, Stochastic Finite Elements: A Spectral Approach, Springer-Verlag, 1991.
• O.P. Le Maitre, O.M. Knio, Spectral Methods for Uncertainty Quantification, Springer, 2010.
• M. M. Dannert: Numerical treatment of imprecise random fields in non-linear solid mechanics, Gottfried Wilhelm Leibniz Universität, Dissertation, 2023.