Der Ingenieurin/dem Ingenieur stehen heute leistungsfähige kommerzielle Finite Element Programmsysteme für die numerische Analyse mechanischer Strukturen zu Verfügung. Ziel dieses Moduls ist es, den Studierenden die theoretischen Grundlagen für diese numerischen Berechnungsmethoden zu vermitteln und sie für kompetente und kritische Anwendung dieser Programmsysteme im Rahmen der linearen Festkörpermechanik vorzubereiten.
Kompetenzerwerb
Im Rahmen dieses Moduls wird eine Einführung in die Finite Elemente Methode (FEM) vermittelt. Nach dem erfolgreichen Abschluss des Kurses sind Studierende in der Lage:
die theoretischen Grundlagen der FEM bei statischen und dynamischen strukturmechanischen Anwendungen zu erläutern und verfügen über ein solides Verständnis der Mechanik als solches,
linear-elastische Verformungs- und Spannungsberechnungen sicher durchzuführen und die Ergebnisse zu interpretieren,
mögliche Fehlerquellen zu benennen und Berechnungsergebnisse unter Berücksichtigung der zugrundegelegten Modellbildung kritisch zu würdigen,
kompetente Vorschläge und Maßnahmen zur Verbesserung der Modelle und konstruktiver Details der untersuchten Systeme zu unterbreiten und konkrete Maßnahmen zur Modellverifikation und Modellvalidierung zu unterbreiten.
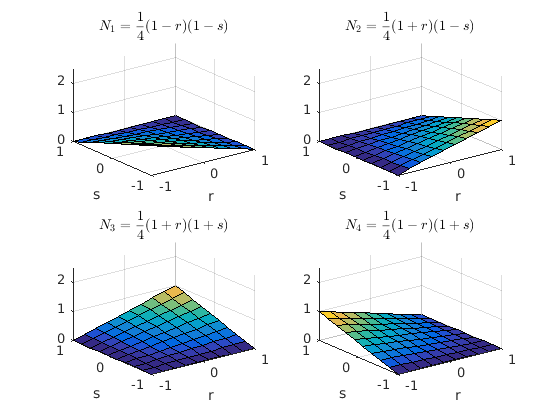
Im Rahmen dieser Lehrveranstaltungen werden die Studierenden an ein kommerzielles Finite Element Programmsystem herangeführt. Die internen Abläufe und Algorithmen werden an einem überschaubaren, auf der Programmiersprache Matlab basierenden Programmsystem erlernt.
Lehrform
Im Wintersemester findet das Modul „Numerische Mechanik“ im Sinne eines Flipped Classroom-Ansatzes statt. Dies bedeutet, dass auf der Lernplattform ILIAS die fachlichen Inhalte zum selbstgesteuerten Eigenstudium aufbereitet sind. Aufbauend darauf unterstützen wir Sie mit Präsenzveranstaltungen wie Impulsvorlesungen, interaktiven Workshops, Tutorien und Gastvorträgen aus der Praxis.
Darüber hinaus kann das Modul jedes Semester als reines Online-Modul belegt werden, d.h. anstelle von Präsenzveranstaltungen gibt es Material und Hilfestellung für das Eigenstudium. Auf der Lernplattform ILIAS stellen wir Ihnen sämtliches Lernmaterial auf Deutsch übersichtlich zur Verfügung.